The convergence is the
angle q between
the optical axis of the lenses. It can be our eyes,
cameras, binoculars, etc... This angle is usually given
in degrees.
When the axis are parallel the
convergence is q = 0.
The formulas about convergence
are:
q = 2 . Atan (0.5 B / D) and D = 0,5 . B / tan(q /2)
|
-
|
-
|
Properties
These are the values of q
and distance D to the convergence center with an inter-
pupillar distance 65 mm..
D
|
0.4
m
|
0.8
m
|
1.2
m
|
1.5
m
|
|
9,3°
|
4,6°
|
3,1°
|
2,4
|
D
|
1.8
m
|
2
m
|
2.5
m
|
3.5
m
|
|
2°
|
1.9°
|
1.5°
|
1.1°
|
D
|
5
m
|
7
m
|
10
m
|
20
m
|
|
0,7°
|
0,5°
|
0,4°
|
0,2°
|
Double the base B is doubling D
keeping the same angle q..
|
-
|
Convergence is set on lens when
shooting. When restituting the pairs, there can be convergence
or divergence depending on the setting when there are two
projectors knowing that the optic laws are the same when
shooting or viewing pictures. Usually it is a problem when
the setting of the projectors is not done properly and that
the disparities are greater than the interocular separation.
In these paragraphs the convergence
at shooting, often ignored, sometimes rejected which is
considered.
|
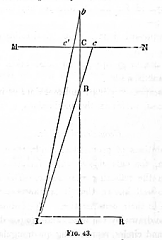
- History
In 1856 Sir David Brewster
in chapter VIII of his book The stereoscope has
the first expressed conditions for stereoscopic photography
(see opposite figure and text)
In this, for portraits at
6 feet distance, 180 cm, the convergence shall not exceed
2°. The calculation confirms that 2° at 180 cm is
a base of 2 1/2 inches, 63 mm. The stereoscopic ratio SR
is calculated for the plan behind at the depth L. The value
of SR range from heighten to strong and is excessive for
L > 2,4 m (4.2 m from the camera)..
- L
|
- 0,6 m
|
- 1 m
|
- 1,5 m
|
- 2.4 m
|
- infini
|
- SR
|
- 22
|
- 32
|
- 40
|
- 50
|
- 87
|
We can only remark the soundly
recommendation of Sir D. Brewster, because in this case
the background was never far, 1 to 3 m as mean value, and
not at infinite distance.
In 1895 in La stéréoscopie
de précision, Louis Cazès described the
convergence. The plan at the horizon and the vertical median
plan between the cameras are reconstitued and homologous.
The other dots are reconstituted by vertical lines but are
horizontally stretched. However, the homologous dots are
close to the coincidence.
Note
.Some stereoscopic cameras are
built with converging lenses. It was done on the Fujifilm
W1. Q
Finally, the relevance of the convergence
relies on the tolerance of perception of the eyes which
is the confusion circle.
|
|
|
In photographic
portraiture the correct angle for a distance
of six feet shall not exceed two degrees. (...)
We come now to consider
under what circumstances the photographer may
place his two cameras at a greater angle
than what we have fixed."
In taking family
portraits for the stereoscope, the cameras must
be placed at an angle of 2° for 6 feet..."
|
The first binocular stereoscopic
cameras with the views on the same glass plate couldn't
have convergence.
In 1923 the Traité
général de stéréoscopie
of Emmanuel Collardeau described a convergence system for
the stereophotography of small objects. He mentioned that
the photographic pair is thoroughly reconstituted by the
eyes. In the same book he mentions the convergence of airplane
aerial pictures.
In 1990 Serge Gauthier published
the Traité et méthodes modernes de stéréoscopie
which is a detailed study of the convergence. He explains
it on well drawn geometric pictures. He establishes the
methodology determining the convergence to apply at each
distance of the first plan.
|
Plans moved closer
The convergence moves the plans
closer to the spectator. If the subject is near and the
background out of focus , convergence on this subject will
emphasize it.
With the convergence, at the same
time than the plans are moved forward, the near objects
are perceived smaller than the same without convergence.
The convergence is also the way
to make blowups.
|
-
|
- Keystone effect
Due to the convergence a plan perpendicular
to the central axis will be seen as trapezoidal by each
lens.. The right side of the pictures will be larger on
the right image and smaller on the left one. It is the other
way on the left side.
It is only discernible on far backgrounds
of wide angle view combined with a strong convergence, which
is not likely.
|
-
Parallel axis
|
|
-
Convergence
|
- The shift of the sides of the edges of the frames is
constant and equal to the base B. It can be disturbing on
near scenes when the base is large.
At short distance
parallelism is disturbing.
The convergence
is necessary for near objects.
|
|
- The shift of the edges of the frames varies. Starting
at first plan it decreases to nought and then increases
until the last plan.
- Note the keystoning
At far distance
a strong convergence may be disturbing.
Practically the
keystoning is seldom perceived.
|
Practically, when
shooting:
The convergence is finally recommanded for the near objects
to the conditions to not exaggerate it and to restrain keystone
and blow up of some seldom scenes.
With field angles greater than
50° a 2° convergence will not disturb the far backgrounds;
on the contrary it will better show nearest objects.
Adjust the convergence is necessary
for the nearest objects and also when zooming field angles
under 30°.
If the background is not far from
the first plan it is favorable to increase the convergence
for the nearest objects.
|
-
|
Not to confuse:
The linear parallax is the disparity
between left and right images. It varies depending on distance
D to the camera and depth L between plans. It has limits
not to exceed.
The linear parallax can be modified
in playback shifting one image. The result is similar to
the convergence, but edges are cropped.
Applied when shooting convergence
shifts all the image like a tracing moved sideways over
a sheet. This is substracting a constant value to all parallax
values. The convergence keeps the full size of the pictures.
|
For a long time I have carefully
follow the parallelism condition commonly recommended. I
controlled precisely the parallelism of the lens axis.
Nowadays I realized that the convergence
don't change the relief effect and its depth but improves
the stereoscopic rendering by avoiding window violation
and keeping the frame of the pictures.
|
|
The binocular stereoscopic cameras
are sometimes built with a permanent slight convergence
between 1 and 2°. This is a convergence center between
1,8 and 4 m.
Many 3D movies are shot with converged
cameras.
|